ころがる剛体と摩擦力(d)

水平面上に、質量{m}、半径{r}、慣性モーメント{I}の円形の物体におき、任意の場所を力{F}で押します。 物体の重心の水平方向の位置を{x}、回転角を{\theta}とします。

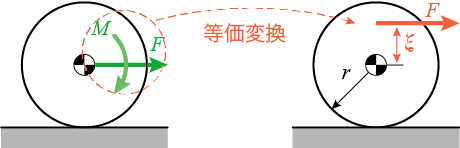
このとき、力には並進運動を変化させる作用と、回転運動を変化させる作用がありますから、力を重心に移動する等価変換を考えると、 力{F}と力のモーメント{M}に分解できます。

f:id:IresAdoheom:20161107194159p:plain:w300

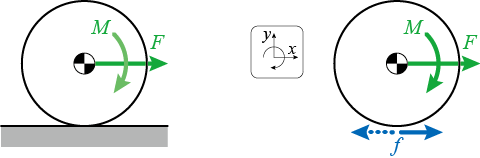
このときの床との間の摩擦力{f}の方向は未定です。

そこで、運動方程式と回転の運動方程式をたててみると、

 {
\begin{align}
\mbox{運動方程式：}\ \ &  F+f\ =\ m\ \ddot{x}\qquad \cdots\ (1) \\
\\
\mbox{回転の運動方程式：}\ \ &  M-fr\ =\  I\ \ddot{\theta} \\
\mbox{(両辺を$r$で割って)}\ \ & \frac{M}{r}-f\ =\ \frac{I}{r}\ \ddot{\theta} \qquad \cdots\ (2) 
\end{align}
}

ここで、(1)+(2)、および(1)-(2)の式を書くと、

{ \begin{align} F+\frac{M}{r}\ &=\ m\ \ddot{x}\ +\ \frac{I}{r}\ \ddot{\theta} \\ 2f+F-\frac{M}{r}\ &=\ m\ \ddot{x}\ -\ \frac{I}{r}\ \ddot{\theta} \end{align} }

すべりなしの条件：{x=r\theta}を代入すると、

{ \begin{align} F+\frac{M}{r}\ &=\ mr\ \ddot{\theta}\ +\ \frac{I}{r}\ \ddot{\theta} \\ 2f+F-\frac{M}{r}\ &=\ mr\ \ddot{\theta}\ -\ \frac{I}{r}\ \ddot{\theta} \end{align} }

物体が円柱の場合には、 {\displaystyle I=\frac{mr^{2}}{2}} なので、整理すると、

 {
\begin{align}
F+\frac{M}{r}\ &=\ \frac{3}{2}mr\ \ddot{\theta} \\
2f+F-\frac{M}{r} &=\ \frac{1}{2}mr\ \ddot{\theta}
\end{align}
}

ここで、２式から、{mr\ \ddot{\theta}}を消去すると、

{ \begin{align} 2f+F-\frac{M}{r} &=\ \frac{1}{3}F+\frac{1}{3}\frac{M}{r} \\ 2f &=\ -\frac{2}{3}F+\frac{4}{3}\frac{M}{r} \end{align} } 

 {\displaystyle
f =\ \frac{2}{3}\frac{M}{r}-\frac{1}{3}F \qquad \cdots\ (3) 
}

力が重心の上方に{\xi}離れた位置に作用すると、{M=F\xi}となり、

f:id:IresAdoheom:20161109132715p:plain:w300
{\displaystyle f =\ \frac{2}{3}\frac{F\xi}{r}-\frac{1}{3}F } 

 {\displaystyle
f =\ \frac{1}{3}\left(2\frac{\xi}{r}-1\right)F \qquad \cdots\ (4) 
}

(注)この式が成り立つのは、基礎的力学の範疇では、{f}が最大静止摩擦力 {f_{max}=\mu N} ({\mu}は静止摩擦係数)より小さい場合となろうかと思います。

【振り返り】(b)および(c)との整合性

(b)の場合、{\xi=0}なので、 {\displaystyle f =-\frac{1}{3}F}となり、{F}と逆向きに働きます。
(c)の場合、{\xi=r}なので、 {\displaystyle f =\frac{1}{3}F}となり、{F}と同じ向きに働きます。

さらには、(4)から{f=0}となる力の作用点が、{\displaystyle \xi=\frac{r}{2}}であることがわかります。

f:id:IresAdoheom:20161110102511p:plain:w400

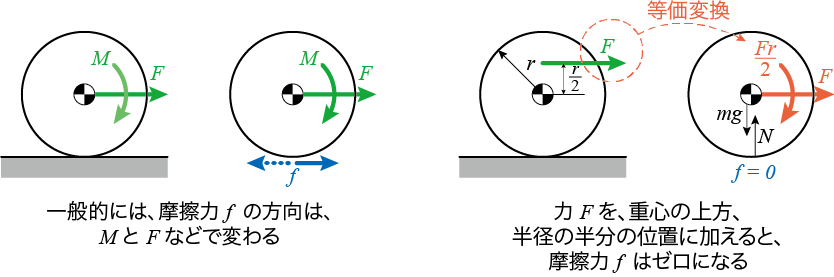
「摩擦力がゼロで回転するのか？」と疑問を持つかもしれませんが、重心から離れた点を押すと、{f=0}でも重心の慣性で回転させることができます。