ころがる剛体と摩擦力(c)

水平面上に、質量{m}、半径{r}、慣性モーメント{I}の円形の物体におき、上部を力{F}で押します。 物体の重心の水平方向の位置を{x}、回転角を{\theta}とします。

f:id:IresAdoheom:20161106113759p:plain:w300

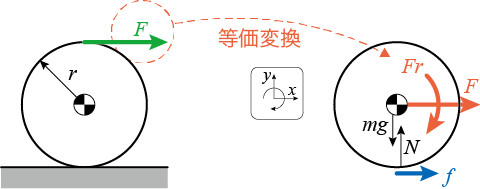
このときも直感的には床との間の摩擦力{f}が図の方向に働くことが予想されますが、これは自明なことなのか、ちょっと迷うところです。

 {
\begin{align}
\mbox{運動方程式：}\ \ &  F+f\ =\ m\ \ddot{x}\qquad \cdots\ (1) \\
\\
\mbox{回転の運動方程式：}\ \ &  Fr-fr\ =\  I\ \ddot{\theta} \\
\mbox{(両辺を$r$で割って)}\ \ & F-f\ =\ \frac{I}{r}\ \ddot{\theta} \qquad \cdots\ (2) 
\end{align}
}

(1)と(2)の辺々をたしあわせると、

 {\displaystyle 2F\ =\ m\ \ddot{x}\ +\ \frac{I}{r}\ \ddot{\theta}\qquad \cdots\ (3)}

物体が円柱の場合には、 {\displaystyle I=\frac{mr^{2}}{2}} なので、整理すると、

{\displaystyle F\ =\ \frac{1}{2}mr\ \ddot{\theta}\ +\ \frac{1}{2}mr\ \ddot{\theta}\ =\ \frac{3}{4}mr\ \ddot{\theta} }

{\theta=x/r}を用いると、

 {\displaystyle 
F\ =\ \frac{3}{4}m\ \ddot{x}\qquad \mbox{または}\ \qquad F\ = \frac{3}{4}mr\ \ddot{\theta}
}

(1)と合わせると、摩擦力の大きさは、{\displaystyle f=\frac{1}{3}F}となります。

【別解】ラグランジアンによる解法

確認のためにラグランジアン{L}からも求めてみます。

物体の運動は、重心の水平方向の位置{x}と回転角{x}を使って表すことができます（一般化座標{(x,\ \theta)}）。
すべりがない場合、ホロノミックな拘束条件は{x-r\theta=0}と表され、ラグランジュの未定係数{\lambda}を用いて、{L}の中に組み込みます。

 {\displaystyle 
L = \frac{1}{2}m\dot{x}^2+\frac{1}{2}I\dot{\theta}^2+\lambda(x-r\theta)
}

一般化座標{(x,\ \theta)}の仮想仕事 {\delta W}を考えるとき、 仮想の変位{\delta x}による仕事と、仮想の変位{\delta \theta}による仕事に別けられ、さらに{\delta x}に共役な一般化力を{Q_x}、{\theta}に共役な一般化力を{Q_\theta}とすると、

{\displaystyle \begin{align} \delta W&=Q_{x}\cdot \delta x + Q_{\theta}\cdot \delta\theta \\ &= F\cdot \delta x + Fr\cdot\delta\theta \end{align} }

となり、{Q_x=F}、{Q_\theta=Fr}となります。

ラグランジュの運動方程式は、

 {\displaystyle 
\begin{align}
\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x} &= m\ddot{x}-\lambda = F \qquad \cdots\ (4)\\
& \\
\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right)-\frac{\partial L}{\partial \theta} &= I\ddot{\theta}+r\lambda = Fr\\
\mbox{(両辺を$r$で割って)} &\ \ \frac{I}{r}\ddot{\theta} - F = -\lambda \qquad \cdots\ (5)
\end{align}
}

(4)と(5)を連立させると、先の解法の答え(3)と同じ式になります。

【振り返り】床においた剛体の回転：力の作用点による仕事の差

振り返ってみると、同じ大きさの力を、重心に加えた場合と、重心からずれた点に加えた場合、

f:id:IresAdoheom:20161109132944p:plain:w300

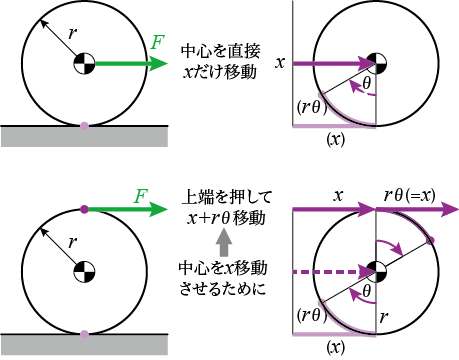
上図のように、重心に力を加えて、{x}だけ動かしたときの仕事は{Fx}だけですが、 下図の場合、重心を{x}動かすには、上端を{x+r\theta=2x}動かす必要があり、その結果の仕事は{F\times 2x}と、倍になってしまいます。
上図と下図の仕事の差は、回転に要する仕事です運動エネルギーの差となって現れます。

今回の設定では、一定の力{F}をどこかに加えて、重心を一定の距離{x}だけ動かすようにしています。着力点をどこにするかによって、重心の変化量は変わります。力を重心に直接加えるのに比べ、上端に力を加えると、倍動かさなければ、同じ量の重心移動は得られません。上端に仕事を余剰に加える分は、円柱の運動エネルギーの増加になります。