ころがる剛体と摩擦力(b)

水平面上に、質量{m}、半径{r}、慣性モーメント{I}の円形の物体がおき、重心を力{F}で押します。 物体の重心の水平方向の位置を{x}、回転角を{\theta}とします。

f:id:IresAdoheom:20161106113750p:plain:w300

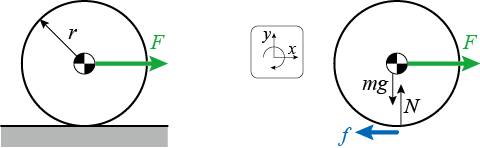
床との接触がなければ並進運動のみが変化し、回転は変化しないのですが、床と接している場合には、直感的に床との間の摩擦力{f}が右図のように働くことがわかります。

 {
\begin{align}
\mbox{運動方程式：}\ \ &  F-f\ =\ m\ \ddot{x}\qquad \cdots\ (1) \\
\\
\mbox{回転の運動方程式：}\ \ &  f\cdot r\ =\  I\ \ddot{\theta} \\
\mbox{(両辺を$r$で割って)}\ \ & f\ =\ \frac{I}{r}\ \ddot{\theta} \qquad \cdots\ (2) 
\end{align}
}

(1)と(2)の辺々をたしあわせると、

 {\displaystyle F\ =\ m\ \ddot{x}\ +\ \frac{I}{r}\ \ddot{\theta}}

物体が円柱の場合には、 {\displaystyle I=\frac{mr^{2}}{2}} なので、整理すると、

{\displaystyle F\ =\ mr\ \ddot{\theta}\ +\ \frac{mr}{2}\ \ddot{\theta}\ =\ \frac{3}{2}mr\ \ddot{\theta} }

すべりなしを仮定して、{\theta=x/r}を用いると、

 {\displaystyle 
F\ =\ \frac{3}{2}m\ \ddot{x}\qquad \mbox{または}\ \qquad F\ = \frac{3}{2}mr\ \ddot{\theta}
}

(2)と合わせると、摩擦力の大きさは、{\displaystyle f=\frac{1}{3}F}となります。