2016-11-07

ころがる剛体と摩擦力(d)

水平面上に、質量 ${m}$ 、半径 ${r}$ 、慣性モーメント ${I}$ の円形の物体におき、任意の場所を力 ${F}$ で押します。物体の重心の水平方向の位置を ${x}$ 、回転角を ${\theta}$ とします。

このとき、力には並進運動を変化させる作用と、回転運動を変化させる作用がありますから、力を重心に移動する等価変換を考えると、力 ${F}$ と力のモーメント ${M}$ に分解できます。

f:id:IresAdoheom:20161107194159p:plain:w300

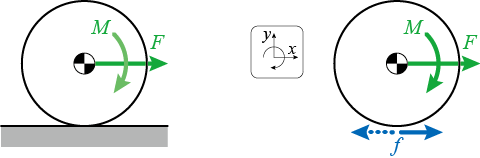
このときの床との間の摩擦力 ${f}$ の方向は未定です。

そこで、運動方程式と回転の運動方程式をたててみると、

ここで、(1)+(2)、および(1)-(2)の式を書くと、

${ \begin{align} F+\frac{M}{r}\ &=\ m\ \ddot{x}\ +\ \frac{I}{r}\ \ddot{\theta} \\ 2f+F-\frac{M}{r}\ &=\ m\ \ddot{x}\ -\ \frac{I}{r}\ \ddot{\theta} \end{align} }$

すべりなしの条件： ${x=r\theta}$ を代入すると、

${ \begin{align} F+\frac{M}{r}\ &=\ mr\ \ddot{\theta}\ +\ \frac{I}{r}\ \ddot{\theta} \\ 2f+F-\frac{M}{r}\ &=\ mr\ \ddot{\theta}\ -\ \frac{I}{r}\ \ddot{\theta} \end{align} }$

物体が円柱の場合には、 $I=\frac{mr^{2}}{2}$ なので、整理すると、

ここで、２式から、 ${mr\ \ddot{\theta}}$ を消去すると、

${ \begin{align} 2f+F-\frac{M}{r} &=\ \frac{1}{3}F+\frac{1}{3}\frac{M}{r} \\ 2f &=\ -\frac{2}{3}F+\frac{4}{3}\frac{M}{r} \end{align} }$

力が重心の上方に ${\xi}$ 離れた位置に作用すると、 ${M=F\xi}$ となり、

f:id:IresAdoheom:20161109132715p:plain:w300

${\displaystyle f =\ \frac{2}{3}\frac{F\xi}{r}-\frac{1}{3}F }$

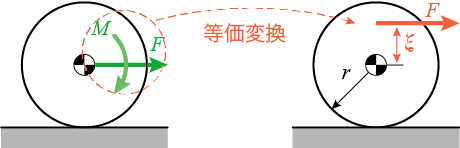
(注)この式が成り立つのは、基礎的力学の範疇では、 ${f}$ が最大静止摩擦力 ${f_{max}=\mu N}$ ( ${\mu}$ は静止摩擦係数)より小さい場合となろうかと思います。

【振り返り】(b)および(c)との整合性

(b)の場合、 ${\xi=0}$ なので、 $f =-\frac{1}{3}F$ となり、 ${F}$ と逆向きに働きます。
(c)の場合、 ${\xi=r}$ なので、 $f =\frac{1}{3}F$ となり、 ${F}$ と同じ向きに働きます。

さらには、(4)から ${f=0}$ となる力の作用点が、 $\xi=\frac{r}{2}$ であることがわかります。

f:id:IresAdoheom:20161110102511p:plain:w400

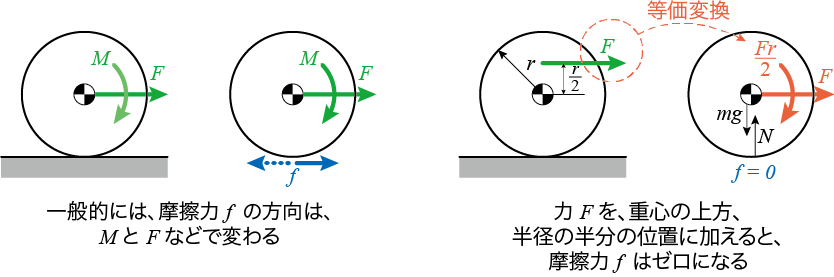
「摩擦力がゼロで回転するのか？」と疑問を持つかもしれませんが、重心から離れた点を押すと、 ${f=0}$ でも重心の慣性で回転させることができます。

2016-11-07

ころがる剛体と摩擦力(c)

水平面上に、質量 ${m}$ 、半径 ${r}$ 、慣性モーメント ${I}$ の円形の物体におき、上部を力 ${F}$ で押します。物体の重心の水平方向の位置を ${x}$ 、回転角を ${\theta}$ とします。

f:id:IresAdoheom:20161106113759p:plain:w300

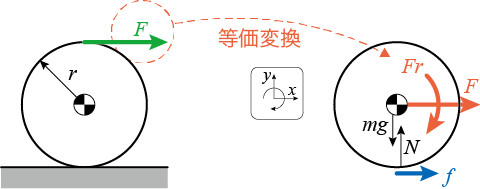
このときも直感的には床との間の摩擦力 ${f}$ が図の方向に働くことが予想されますが、これは自明なことなのか、ちょっと迷うところです。

(1)と(2)の辺々をたしあわせると、

物体が円柱の場合には、 $I=\frac{mr^{2}}{2}$ なので、整理すると、

${\displaystyle F\ =\ \frac{1}{2}mr\ \ddot{\theta}\ +\ \frac{1}{2}mr\ \ddot{\theta}\ =\ \frac{3}{4}mr\ \ddot{\theta} }$

${\theta=x/r}$ を用いると、

(1)と合わせると、摩擦力の大きさは、 $f=\frac{1}{3}F$ となります。

【別解】ラグランジアンによる解法

確認のためにラグランジアン ${L}$ からも求めてみます。

物体の運動は、重心の水平方向の位置 ${x}$ と回転角 ${x}$ を使って表すことができます（一般化座標 ${(x,\ \theta)}$ ）。
すべりがない場合、ホロノミックな拘束条件は ${x-r\theta=0}$ と表され、ラグランジュの未定係数 ${\lambda}$ を用いて、 ${L}$ の中に組み込みます。

一般化座標 ${(x,\ \theta)}$ の仮想仕事 ${\delta W}$ を考えるとき、仮想の変位 ${\delta x}$ による仕事と、仮想の変位 ${\delta \theta}$ による仕事に別けられ、さらに ${\delta x}$ に共役な一般化力を ${Q_x}$ 、 ${\theta}$ に共役な一般化力を ${Q_\theta}$ とすると、

${\displaystyle \begin{align} \delta W&=Q_{x}\cdot \delta x + Q_{\theta}\cdot \delta\theta \\ &= F\cdot \delta x + Fr\cdot\delta\theta \end{align} }$

となり、 ${Q_x=F}$ 、 ${Q_\theta=Fr}$ となります。

ラグランジュの運動方程式は、

(4)と(5)を連立させると、先の解法の答え(3)と同じ式になります。

【振り返り】床においた剛体の回転：力の作用点による仕事の差

振り返ってみると、同じ大きさの力を、重心に加えた場合と、重心からずれた点に加えた場合、

f:id:IresAdoheom:20161109132944p:plain:w300

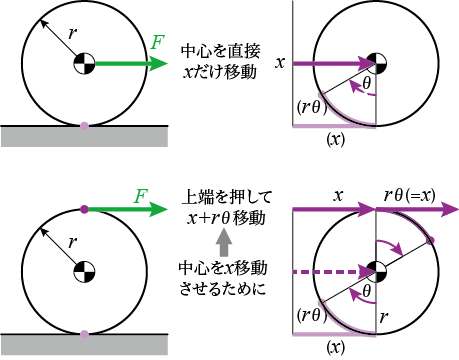
上図のように、重心に力を加えて、 ${x}$ だけ動かしたときの仕事は ${Fx}$ だけですが、下図の場合、重心を ${x}$ 動かすには、上端を ${x+r\theta=2x}$ 動かす必要があり、その結果の仕事は ${F\times 2x}$ と、倍になってしまいます。
上図と下図の仕事の差は、~~回転に要する仕事です~~運動エネルギーの差となって現れます。

今回の設定では、一定の力 ${F}$ をどこかに加えて、重心を一定の距離 ${x}$ だけ動かすようにしています。着力点をどこにするかによって、重心の変化量は変わります。力を重心に直接加えるのに比べ、上端に力を加えると、倍動かさなければ、同じ量の重心移動は得られません。上端に仕事を余剰に加える分は、円柱の運動エネルギーの増加になります。

2016-11-06

ころがる剛体と摩擦力(b)補足

ころがる剛体に摩擦力が働くのはよいのですが、床に剛体が点接触する時、すべりなしの条件では、摩擦力は仕事をしません。

この理由を明確に書くのは難しいのですが、半径 ${r}$ 、回転角 ${\theta}$ の円板上の点 ${P}$ の軌跡を調べてみると理解できます。
f:id:IresAdoheom:20161106210205p:plain
${P}$ の座標を ${(X,\ Y)}$ 、重心の座標を ${(x,\ y)}$ とすると、すべりなしの条件下では ${x=r\theta,\ y=r}$ の関係を用いて、

この ${(X,\ Y)}$ の軌跡は、サイクロイド曲線と呼ばれ、図の赤い軌跡となります。

時刻 ${t}$ で微分すると、

${\displaystyle \begin{align} \dot{X}\ &=\ r(\dot{\theta}-cos\theta\cdot\dot{\theta}) =r\dot{\theta}(1-cos\theta) \\ \dot{Y}\ &=\ r\ \sin\theta\cdot\dot{\theta} \end{align} }$

ですが、特に床との接点( ${\theta=0}$ )では、 ${\dot{X}=0}$ となります。
接点での速度は

${\displaystyle \dot{X}=\frac{dX}{dt}=0 }$

ですから、接触している微小な時間 ${dt}$ の間の点 ${P}$ の変位 ${dX}$ は

${\displaystyle dX=0 }$

で、接触して摩擦力は働くものの、変位がゼロなので、剛体円板（球）が床にすべりなく接触するときの

摩擦力による仕事

となります（こんな説明でいいのか、自信なし）。

2016-11-06

ころがる剛体と摩擦力(b)

水平面上に、質量 ${m}$ 、半径 ${r}$ 、慣性モーメント ${I}$ の円形の物体がおき、重心を力 ${F}$ で押します。物体の重心の水平方向の位置を ${x}$ 、回転角を ${\theta}$ とします。

f:id:IresAdoheom:20161106113750p:plain:w300

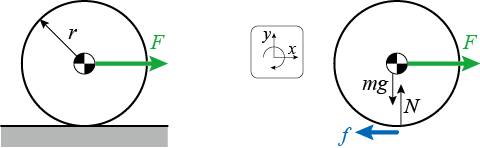
床との接触がなければ並進運動のみが変化し、回転は変化しないのですが、床と接している場合には、直感的に床との間の摩擦力 ${f}$ が右図のように働くことがわかります。

(1)と(2)の辺々をたしあわせると、

物体が円柱の場合には、 $I=\frac{mr^{2}}{2}$ なので、整理すると、

${\displaystyle F\ =\ mr\ \ddot{\theta}\ +\ \frac{mr}{2}\ \ddot{\theta}\ =\ \frac{3}{2}mr\ \ddot{\theta} }$

すべりなしを仮定して、 ${\theta=x/r}$ を用いると、

(2)と合わせると、摩擦力の大きさは、 $f=\frac{1}{3}F$ となります。

2016-11-06

ころがる剛体と摩擦力(a)

質量 ${m}$ 、半径 ${r}$ 、慣性モーメント ${I}$ の円形の物体に、重力が働かない空間で、ひもを巻きつけた物体を接線方向に力 ${F}$ で引張ります。物体の重心の水平方向の位置を ${x}$ 、回転角を ${\theta}$ とします。

f:id:IresAdoheom:20161106113741p:plain:w300

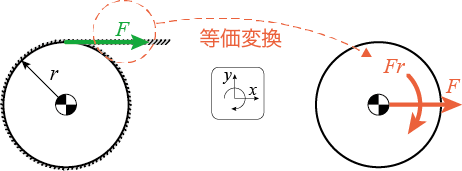
${F}$ を等価変換して、重心に作用する並進力 ${F}$ と、力のモーメント ${Fr}$ に分解しています。

(1)と(2)を連立させると、

物体が円柱の場合には、 $I=\frac{mr^{2}}{2}$ なので、整理すると、

$\ddot{x}\ =\ \frac{r}{2}\ \ddot{\theta}$

　
初期位置、初期速度、初期角度、初期角速度がすべてゼロとすれば、

2016-11-06

ころがる剛体と摩擦力(最初)

子供に質問されてシドロモドロだったので、剛体の球とか円柱がころがるとき、発生する摩擦力の性質についての説明を考えました。
まずは、すべりなしの場合の次の４つの図から。

質量 ${m}$ 、半径 ${r}$ 、慣性モーメント ${I}$ の円形の物体に、色々な力 ${F}$ を加えた場合について、物体の重心の水平方向の位置を ${x}$ 、回転角を ${\theta}$ とします。

f:id:IresAdoheom:20161105225842p:plain

(a)では、重力が働かない空間で、ひもを巻きつけた物体を、接線方向に力 ${F}$ で引張っています。
力 ${F}$ は重心からずれた位置に作用しますので、並進運動を変化させる効果と回転運動を変化させる効果を持ちます（等価変換して、力を重心に作用させるとわかりやすい）が、床に接しておらず、摩擦力が働きません。

(b)では、水平面上に置かれた物体の重心を力 ${F}$ で押しています。
床との接触がなければ並進運動のみが変化し、回転は変化しないのですが、床と接している場合には、直感的に床との間の摩擦力 ${f}$ が(b)下図のように働くことがわかります。

(c)では、水平面上に置かれた物体の上部を力 ${F}$ で押しています。
このときも直感的には床との間の摩擦力 ${f}$ が(c)下図の方向に働くことが予想されますが、これは自明なことなのか、ちょっと迷うところです。

(d)は、(b)と(c)を一般化して、重心に力 ${F}$ と、力のモーメント ${M}$ が作用する場合です。
(c)で迷った摩擦力 ${f}$ について、数式で判断できないのか、考えてみます。

次の記事以降で注意して書きたいところ： 
   
　●　(a)と(c)から、剛体がころがるときには点接触で摩擦力が発生する  
  
　●　(b)と(c)から、力を偏心したとき、力による仕事量が変化する  
  
　●　(b)と(c)の摩擦力の方向は(d)を使って判定する

2015-05-06

やる気でも出すか

といってはみるものの、簡単に出たら苦労しないんだなぁ。

ところが、このＧＷ、結構やる気を出すことに成功。

新しい小道具は「If-then planning」。

本来の使い方とは少し違うようだけど、効果がありました。

（例題）「洗い物をしなくっちゃ・・・あとで」を今やるには、

　　　　「もし、食事が終わったら、洗い物をしなくっちゃ」

　　　　「もし、食事が終わったら、」

そう、やることの前に、

　　　　「いつ」や「どこで」などの条件を、「もし・・・なら」の構文でつけてみる

だけです。

体が動かないときは、

　　　　「もし」構文を繰り返す、

　　　　　だんだん大きく繰り返す、

　　　　　何するかをなくしても繰り返す

不思議なことに、掃除、洗濯、炊事も順調にクリアー！

どんな心理学的作用かわかんないのですが、意識が「目的の行動」からそれて、実行への心のハードルが下がったの？

誤解のないように、本来の使い方を簡単に紹介。

KOPi Diary

ころがる剛体と摩擦力(d)

${ \begin{align} \mbox{運動方程式：}\ \ & F+f\ =\ m\ \ddot{x}\qquad \cdots\ (1) \\ \\ \mbox{回転の運動方程式：}\ \ & M-fr\ =\ I\ \ddot{\theta} \\ \mbox{(両辺を$r$で割って)}\ \ & \frac{M}{r}-f\ =\ \frac{I}{r}\ \ddot{\theta} \qquad \cdots\ (2) \end{align} }$

${ \begin{align} F+\frac{M}{r}\ &=\ m\ \ddot{x}\ +\ \frac{I}{r}\ \ddot{\theta} \\ 2f+F-\frac{M}{r}\ &=\ m\ \ddot{x}\ -\ \frac{I}{r}\ \ddot{\theta} \end{align} }$

${ \begin{align} F+\frac{M}{r}\ &=\ mr\ \ddot{\theta}\ +\ \frac{I}{r}\ \ddot{\theta} \\ 2f+F-\frac{M}{r}\ &=\ mr\ \ddot{\theta}\ -\ \frac{I}{r}\ \ddot{\theta} \end{align} }$

${ \begin{align} F+\frac{M}{r}\ &=\ \frac{3}{2}mr\ \ddot{\theta} \\ 2f+F-\frac{M}{r} &=\ \frac{1}{2}mr\ \ddot{\theta} \end{align} }$

${ \begin{align} 2f+F-\frac{M}{r} &=\ \frac{1}{3}F+\frac{1}{3}\frac{M}{r} \\ 2f &=\ -\frac{2}{3}F+\frac{4}{3}\frac{M}{r} \end{align} }$

${\displaystyle f =\ \frac{2}{3}\frac{M}{r}-\frac{1}{3}F \qquad \cdots\ (3) }$

${\displaystyle f =\ \frac{2}{3}\frac{F\xi}{r}-\frac{1}{3}F }$

${\displaystyle f =\ \frac{1}{3}\left(2\frac{\xi}{r}-1\right)F \qquad \cdots\ (4) }$

【振り返り】(b)および(c)との整合性

ころがる剛体と摩擦力(c)

${ \begin{align} \mbox{運動方程式：}\ \ & F+f\ =\ m\ \ddot{x}\qquad \cdots\ (1) \\ \\ \mbox{回転の運動方程式：}\ \ & Fr-fr\ =\ I\ \ddot{\theta} \\ \mbox{(両辺を$r$で割って)}\ \ & F-f\ =\ \frac{I}{r}\ \ddot{\theta} \qquad \cdots\ (2) \end{align} }$

$2F\ =\ m\ \ddot{x}\ +\ \frac{I}{r}\ \ddot{\theta}\qquad \cdots\ (3)$

${\displaystyle F\ =\ \frac{1}{2}mr\ \ddot{\theta}\ +\ \frac{1}{2}mr\ \ddot{\theta}\ =\ \frac{3}{4}mr\ \ddot{\theta} }$

${\displaystyle F\ =\ \frac{3}{4}m\ \ddot{x}\qquad \mbox{または}\ \qquad F\ = \frac{3}{4}mr\ \ddot{\theta} }$

【別解】ラグランジアンによる解法

${\displaystyle L = \frac{1}{2}m\dot{x}^2+\frac{1}{2}I\dot{\theta}^2+\lambda(x-r\theta) }$

${\displaystyle \begin{align} \delta W&=Q_{x}\cdot \delta x + Q_{\theta}\cdot \delta\theta \\ &= F\cdot \delta x + Fr\cdot\delta\theta \end{align} }$

【振り返り】床においた剛体の回転：力の作用点による仕事の差

ころがる剛体と摩擦力(b)補足

${ \begin{align} X\ &=\ x-r\ sin\theta\ =\ r\theta\ -\ r\ sin\theta\ =\ r(\theta\ -sin\theta) \\ Y\ &=\ y-r\ cos\theta = r-r\ cos\theta =r(1-cos\theta) \end{align} }$

${\displaystyle \begin{align} \dot{X}\ &=\ r(\dot{\theta}-cos\theta\cdot\dot{\theta}) =r\dot{\theta}(1-cos\theta) \\ \dot{Y}\ &=\ r\ \sin\theta\cdot\dot{\theta} \end{align} }$

${\displaystyle \dot{X}=\frac{dX}{dt}=0 }$

${\displaystyle dX=0 }$

摩擦力による仕事 ${\displaystyle f\cdot dX=0 }$

ころがる剛体と摩擦力(b)

${ \begin{align} \mbox{運動方程式：}\ \ & F-f\ =\ m\ \ddot{x}\qquad \cdots\ (1) \\ \\ \mbox{回転の運動方程式：}\ \ & f\cdot r\ =\ I\ \ddot{\theta} \\ \mbox{(両辺を$r$で割って)}\ \ & f\ =\ \frac{I}{r}\ \ddot{\theta} \qquad \cdots\ (2) \end{align} }$

$F\ =\ m\ \ddot{x}\ +\ \frac{I}{r}\ \ddot{\theta}$

${\displaystyle F\ =\ mr\ \ddot{\theta}\ +\ \frac{mr}{2}\ \ddot{\theta}\ =\ \frac{3}{2}mr\ \ddot{\theta} }$

${\displaystyle F\ =\ \frac{3}{2}m\ \ddot{x}\qquad \mbox{または}\ \qquad F\ = \frac{3}{2}mr\ \ddot{\theta} }$

ころがる剛体と摩擦力(a)

${ \begin{align} \mbox{運動方程式：}\ \ & F\ =\ m\ \ddot{x}\qquad \cdots\ (1) \\ \\ \mbox{回転の運動方程式：}\ \ & F\cdot r\ =\ I\ \ddot{\theta} \\ \mbox{(両辺を$r$で割って)}\ \ & F\ =\ \frac{I}{r}\ \ddot{\theta} \qquad \cdots\ (2) \end{align} }$

$m\ \ddot{x}\ =\ \frac{I}{r}\ \ddot{\theta}$

$\ddot{x}\ =\ \frac{r}{2}\ \ddot{\theta}$

$x\ =\ \frac{r\theta}{2}\$

ころがる剛体と摩擦力(最初)

やる気でも出すか